SOBRE NOSOTRAS

Hola, somos las amichis de la UCV, actualmente cursando la carrera de Educación Preescolar y Primera Etapa de Básica, en nuestro blog les expondremos sobre el tema de las fracciones dedicado para nuestros alumnos de Educación Básica, en el cual explicaremos lo mejor posible de los contenidos de las fracciones.

ACTIVIDAD PARA EL GRUPO

        Antes de realizar estos ejercicios, observa la definición de fracción, los tipos y las diferentes operaciones (suma, resta, multiplicación, división) con las fracciones, para certificar que has aprendido a realizar esto con soltura.

            A continuación, ponemos este ejercicio-resumen para que lo practiquen:

Ejercicio para practicar

         Posteriormente, les presentamos un vídeo interactivo en el cual para participar solo debes pensar cuál puede ser el resultado a lo que se te pregunte, debes estar atento, sino, no te dará tiempo de pensar.

   Una vez visto el video... Responde:

•  ¿Que significan las fracciones? 
• ¿Cuáles son los tipos de fracciones? 
• ¿Cuáles son las diferentes operaciones?

         Cuando termines de realizar la actividad anterior, te invitamos a colocar un comentario, ya sean preguntas, inquietudes o  críticas con el fin del mejoramiento de nuestra presentación. 

REFERENCIAS BIBLIOGRAFICAS

       En este blog hemos visitado la página web de www.wikipedia.com pero, principalmente, los conocimientos previos que teníamos de las fracciones desde que estábamos en educación básica. Esto nos ha ayudado a expresar nuestros conocimientos de una manera más práctica y sencilla de la que vienen en los libros de textos.

         También consultamos la página de música y video: www.youtube.com, la cual nos ha facilitado a través de sus vídeos la explicación dinámica de nuestro contenido.

CONCLUSIÓN

       Como conclusión, decir que para desarrollar las competencias de las fracciones, debemos aplicar la teoría a la práctica, es decir, mediante juegos y vídeos divertidos se hace más amena la comprensión de este tipo de contenidos y, también, los asimilamos mejor. 

OPERACIONES DE FRACCIONES

 A continuación les mostraremos algunos ejemplos sobre las operaciones de suma, resta, multiplicación y división de fracciones, para que sea de mayor comprensión las operaciones.

TIPOS DE FRACCIONES

       A continuación se presentará a través de este video un resumen de los diferentes tipos de fracciones entre ellas se destacan: Fracción Propia, Impropia, Reducible, Irreducible, Homogénea, Heterogénea, Equivalente, como Porcentaje y Mixta.

Fracción propia

       Una fracción propia es aquella en que el denominador es mayor que el numerador, es decir, el resultado de la división del numerador por el denominador es menor que 1. Por ejemplo: 1/3, 2/8, 5/6.

Fracción impropia

       Una fracción impropia es aquella en donde el numerador es mayor que el denominador, es decir, el resultado de la división del numerador por el denominador es mayor que 1. Por ejemplo: 4/3, 6/3, 5/4.

Fracción reducible

       Una fracción reducible es aquella en la que el numerador y el denominador no son primos entre sí y puede ser simplificada. Por ejemplo: 10/4 puede ser simplificada a 5/2 y en este caso, sí serían primos entre sí.

Fracción irreducible

       Una fracción irreducible es aquella en la que el numerador y el denominador son primos entre sí y, por tanto, no puede ser simplificada. Por ejemplo: 7/5, 3/4, 5/3.

Fracción homogénea

      Unas fracciones homogéneas son aquellas que tienen el mismo denominador. Por ejemplo, 3/4 y 1/4, 7/5 y 2/5.

Fracción heterogénea

       Las fracciones heterogéneas son aquellas que tienen distinto denominador. Por ejemplo, 1/4 y 3/5, 6/7 y 2/9,… Todas estas fracciones no tienen denominador igual sino que son diferentes entre sí, es decir, 4 y 5, 7 y 9 no son iguales entre sí, por lo que, son Fracciones heterogéneas.

Fracción equivalente

    Una fracción equivalente es aquella que tiene el mismo valor que otra dada, es decir, si al reducir la fracción mayor en una menor es igual que la menor, éstas son fracciones equivalentes. Por ejemplo: 1/2, 2/4, 3/6 y 4/8 son equivalentes, porque el último es cuatro veces la primera, la tercera es tres veces la primera y la segunda es el doble que la primera.

Fracción como porcentaje

     Un porcentaje es una forma de expresar un número como una fracción de 100: utilizando el signo porcentaje %, que se debe escribir inmediatamente después del número al que se refiere, sin dejar espacio de separación.

        Ejemplo: La expresión de un número por mil (1.000‰), es una manera de expresarlo como una fracción de 1.000, o como la décima parte de un porcentaje; se escribe con el signo ‰.

Fracción mixta

       Una fracción mixta es aquella que es una suma abreviada de un entero y una fracción propia, es decir, un número como 1 y después una fracción en la que el numerador es menor que el denominador. Por ejemplo. 1 1/3, esto sería 3/3 + 1/3, en total, 4/3 sería el resultado final.

CLASIFICACIÓN DE FRACCIONES

       Las fracciones se pueden clasificar dependiendo de si el cociente de los dos presenta decimales o no. Si no los presenta, estaremos en el caso de las fracciones enteras. Si presenta decimales estaremos en el caso de fracciones decimales, ya sean exactas o periódicas. 

Fracción entera

       Es aquella en el que el numerador y el denominador son iguales o el numerador es múltiplo del denominador. Como consecuencia, en la división entre los dos números el resto es 0. Por ejemplo: 2/2 y 3/3 son fracciones exactas en las tanto el numerador como el denominador es el mismo número y, en las fracciones 4/2 y 9/3, por ejemplo, los numeradores son múltiplos de los denominadores, 4 es múltiplo de 2 (2·2=4) y 9 es múltiplo de 3 (3·3=9).

Fracción decimal

       Una fracción decimal es una fracción del tipo , es decir, una fracción cuyo denominador es una potencia de 10. Por convención, se toma a positiva. Las fracciones decimales suelen expresarse sin denominador, con uso del separador decimal, es decir, como número decimal exacto (Por ejemplo: 8/10, 83/100, 83/1000 y 8/10000 se escriben 0.8, 0.83, 0.083 y 0.0008).

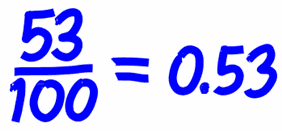
Fracción decimal exacta

       Es una fracción que al realizar la división entre el numerador y el denominador presenta un límite de decimales. Por ejemplo, si tenemos la división de 3/4 sale 0,75, es decir, tiene un número finito de decimales y, por lo tanto, es una fracción decimal exacta.

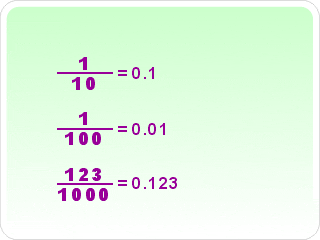
Fracción decimal periódica

       Una fracción decimal periódica es aquella en el que la división entre el numerador y el denominador tiene como resultado un número determinado de decimales que se repiten continuamente, es decir, es un número con infinidad de decimales pero que un grupo de cifras se repite continuamente. Por ejemplo, 2/3 al dividirlos te sale 0,66666666666666, entonces 2/3 sería una fracción decimal periódica.

CONCEPTO

        Una fracción, o número fraccionario, o quebrado es la expresión de una cantidad dividida entre otra; es decir que representa un cociente no efectuado de números. Por razones históricas también se les llama fracción común, fracción vulgar o fracción decimal. El conjunto matemático que contiene a las fracciones es el conjunto de los números racionales.

• El concepto de numerador y denominador:

       El número 3 es el numerador y el 4 es el denominador, es decir, el número de arriba de la línea es el numerador y el número de abajo de la línea es el denominador. La línea que existe entre ellas se llama línea divisoria. El numerador se refiere al número de elementos que se van a repartir y el denominador se refiere al número de partes por las que se va a dividir. Es la representación gráfica de una división, en el que puede ser exacta, periódico puro y periódico mixto, en la que lo explicaré posteriormente.

Representación gráfica de 3/4:

       A continuación presentaremos un vídeo en el que resume lo que es una fracción mediante frutas y las porciones que se pueden expresar mediante fracciones. También abordaremos los número mixtos, fracciones equivalentes y fracciones impropias, todo esto se expondrá más adelante.